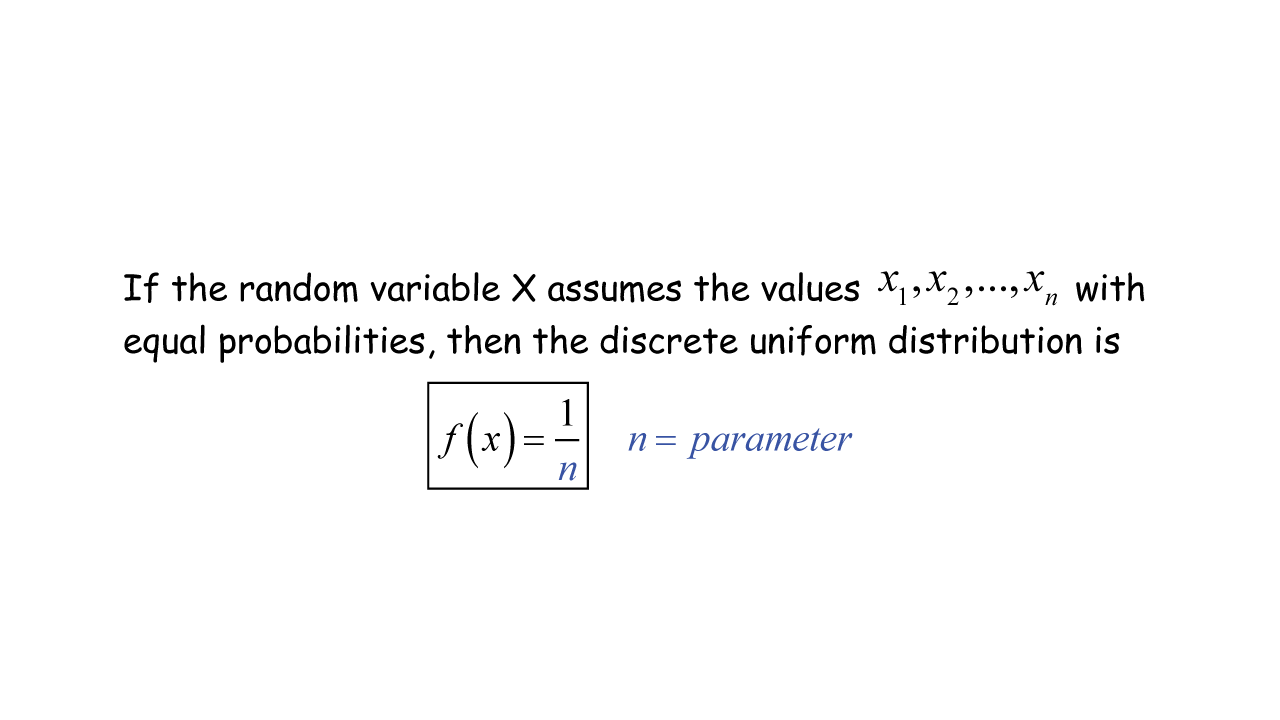 Probabilities in general can be found using the Basic Probabality Calculator. We also acknowledge previous National Science Foundation support under grant numbers 1246120, 1525057, and 1413739. What is the 90th percentile of square footage for homes? b. WebThe discrete uniform distribution s a discrete probability distribution that can be characterized by saying that all values of a finite set of possible values are equally VrcAcademy - 2020About Us | Our Team | Privacy Policy | Terms of Use. This means you will have to find the value such that \(\frac{3}{4}\), or 75%, of the cars are at most (less than or equal to) that age. \(P(x < k) = 0.30\) The mean of \(X\) is \(\mu = \frac{a+b}{2}\). Write the distribution in proper notation, and calculate the theoretical mean and standard deviation. MGF of discrete uniform distribution is given by ruth benjamin paris; spanish pottery makers; where is les gray buried; how to cook golden wonder potatoes Thus, the cumulative distribution function is: F X(x) = x U (z;a,b)dz (4) (4) F X ( x) = x U ( z; a, b) d z Find the probability that a randomly selected furnace repair requires more than two hours. The variance of above discrete uniform random variable is $V(X) = \dfrac{(b-a+1)^2-1}{12}$. Solve the problem two different ways (see Example). All values \(x\) are equally likely.
Probabilities in general can be found using the Basic Probabality Calculator. We also acknowledge previous National Science Foundation support under grant numbers 1246120, 1525057, and 1413739. What is the 90th percentile of square footage for homes? b. WebThe discrete uniform distribution s a discrete probability distribution that can be characterized by saying that all values of a finite set of possible values are equally VrcAcademy - 2020About Us | Our Team | Privacy Policy | Terms of Use. This means you will have to find the value such that \(\frac{3}{4}\), or 75%, of the cars are at most (less than or equal to) that age. \(P(x < k) = 0.30\) The mean of \(X\) is \(\mu = \frac{a+b}{2}\). Write the distribution in proper notation, and calculate the theoretical mean and standard deviation. MGF of discrete uniform distribution is given by ruth benjamin paris; spanish pottery makers; where is les gray buried; how to cook golden wonder potatoes Thus, the cumulative distribution function is: F X(x) = x U (z;a,b)dz (4) (4) F X ( x) = x U ( z; a, b) d z Find the probability that a randomly selected furnace repair requires more than two hours. The variance of above discrete uniform random variable is $V(X) = \dfrac{(b-a+1)^2-1}{12}$. Solve the problem two different ways (see Example). All values \(x\) are equally likely.  \nonumber \]. The data that follow are the number of passengers on 35 different charter fishing boats. a. Get the result! The hypergeometric probabiity distribution is very similar to the binomial probability distributionn. Then \(X \sim U(6, 15)\). So, \(P(x > 12|x > 8) = \frac{(x > 12 \text{ AND } x > 8)}{P(x > 8)} = \frac{P(x > 12)}{P(x > 8)} = \frac{\frac{11}{23}}{\frac{15}{23}} = \frac{11}{15}\). \(P(x < 4) =\) _______. Considering only the cars less than 7.5 years old, find the probability that a randomly chosen car in the lot was less than four years old. \end{eqnarray*} $$, A general discrete uniform distribution has a probability mass function, $$ The histogram that could be constructed from the sample is an empirical distribution that closely matches the theoretical uniform distribution. (In other words: find the minimum time for the longest 25% of repair times.) Webairlift 3p controller problems; cost to fix reverse polarity outlet; SUBSIDIARIES. Since the probability in the first case is 0.9997 and in the second case is \(1-0.9997=0.0003\), the probability distribution for \(X\) is: \[\begin{array}{c|cc} x &195 &-199,805 \\ \hline P(x) &0.9997 &0.0003 \\ \end{array}\nonumber \], \[\begin{align*} E(X) &=\sum x P(x) \\[5pt]&=(195)\cdot (0.9997)+(-199,805)\cdot (0.0003) \\[5pt] &=135 \end{align*} \nonumber \]. \(f(x) = \frac{1}{9}\) where \(x\) is between 0.5 and 9.5, inclusive. The graph illustrates the new sample space. These can be written in terms of the Heaviside step function as. Find the probability. Ninety percent of the time, a person must wait at most 13.5 minutes. Find the probability that the number appear on the top is less than 3.
\nonumber \]. The data that follow are the number of passengers on 35 different charter fishing boats. a. Get the result! The hypergeometric probabiity distribution is very similar to the binomial probability distributionn. Then \(X \sim U(6, 15)\). So, \(P(x > 12|x > 8) = \frac{(x > 12 \text{ AND } x > 8)}{P(x > 8)} = \frac{P(x > 12)}{P(x > 8)} = \frac{\frac{11}{23}}{\frac{15}{23}} = \frac{11}{15}\). \(P(x < 4) =\) _______. Considering only the cars less than 7.5 years old, find the probability that a randomly chosen car in the lot was less than four years old. \end{eqnarray*} $$, A general discrete uniform distribution has a probability mass function, $$ The histogram that could be constructed from the sample is an empirical distribution that closely matches the theoretical uniform distribution. (In other words: find the minimum time for the longest 25% of repair times.) Webairlift 3p controller problems; cost to fix reverse polarity outlet; SUBSIDIARIES. Since the probability in the first case is 0.9997 and in the second case is \(1-0.9997=0.0003\), the probability distribution for \(X\) is: \[\begin{array}{c|cc} x &195 &-199,805 \\ \hline P(x) &0.9997 &0.0003 \\ \end{array}\nonumber \], \[\begin{align*} E(X) &=\sum x P(x) \\[5pt]&=(195)\cdot (0.9997)+(-199,805)\cdot (0.0003) \\[5pt] &=135 \end{align*} \nonumber \]. \(f(x) = \frac{1}{9}\) where \(x\) is between 0.5 and 9.5, inclusive. The graph illustrates the new sample space. These can be written in terms of the Heaviside step function as. Find the probability. Ninety percent of the time, a person must wait at most 13.5 minutes. Find the probability that the number appear on the top is less than 3.  Define the random variable and the element p in [0,1] of the p-quantile. This means that any smiling time from zero to and including 23 seconds is equally likely. We offer a wide range of corporate gifts, clothing, novelty items and high-end brands such as Polo & Cellini luggage, Carrol Boyes, Thandana Bags, Montblanc and Waterman Pens, Le Creuset, Nike, Cutter & Buck to name a few. b. a. Find the probability that a randomly selected student needs at least eight minutes to complete the quiz. What has changed in the previous two problems that made the solutions different. Then \(X \sim U(0.5, 4)\). For the first way, use the fact that this is a conditional and changes the sample space. Find the expected value of \(X\), and interpret its meaning. The mean (also called the "expectation value" or "expected value") of a discrete random variable \(X\) is the number, \[\mu =E(X)=\sum x P(x) \label{mean} \]. Calculates moment number t using the moment generating function. Vary the parameters and note the graph of the distribution function. Hope you like article on Discrete Uniform Distribution. How to Input Let the random variable $X$ have a discrete uniform distribution on the integers $9\leq x\leq 11$. WebThe value of the CDF can be calculated by using the discrete probability distribution. Web(Discrete uniform distribution) A discrete random variable is said to be uniformly distributed. State the values of a and \(b\). The expected value of discrete uniform random variable is $E(X) =\dfrac{N+1}{2}$. Here are examples of how discrete and continuous uniform distribution differ: Discrete example. Accessibility StatementFor more information contact us atinfo@libretexts.orgor check out our status page at https://status.libretexts.org. The probability that the last digit of the selected number is 6, $$ \begin{aligned} P(X=6) &=\frac{1}{10}\\ &= 0.1 \end{aligned} $$, b. \end{aligned} $$. What is the probability density function? Like the variance, the standard deviation is a measure of variability for a discrete random variable. All rights are reserved. Probabilities for discrete probability distributions can be found using the Discrete Accessibility StatementFor more information contact us atinfo@libretexts.orgor check out our status page at https://status.libretexts.org. The probability of x successes in n trials is given by the binomial probability function. In other words, a discrete probability distribution doesnt include any values with a probability of zero. WebDiscrete Uniform Distribution Calculator. Each of these numbers corresponds to an event in the sample space \(S=\{hh,ht,th,tt\}\) of equally likely outcomes for this experiment: \[X = 0\; \text{to}\; \{tt\},\; X = 1\; \text{to}\; \{ht,th\}, \; \text{and}\; X = 2\; \text{to}\; {hh}. \end{aligned} $$. The MGF of $X$ is $M_X(t) = \dfrac{e^t (1 - e^{tN})}{N (1 - e^t)}$. Uniform Distribution between 1.5 and 4 with an area of 0.25 shaded to the right representing the longest 25% of repair times. r(Z/ Interpret the Output Get the result! why did aunjanue ellis leave the mentalist; carmine's veal saltimbocca recipe Another method is to create a graph with the values of x on the horizontal axis and the values of f(x) on the vertical axis. Control list size (generate up to 10,000 random numbers). \(X= 2\) is the event \(\{11\}\), so \(P(2)=1/36\). The data follow a uniform distribution where all values between and including zero and 14 are equally likely. Choose a distribution. Standard Deviation Sketch the graph of the probability distribution. 6b. To learn more about other discrete probability distributions, please refer to the following tutorial: Let me know in the comments if you have any questions on Discrete Uniform Distribution Examples and your thought on this article. The probability mass function of $X$ is, $$ \begin{aligned} P(X=x) &=\frac{1}{9-0+1} \\ &= \frac{1}{10}; x=0,1,2\cdots, 9 \end{aligned} $$, a. Mean median mode calculator for grouped data. obtained by dividing both sides by 0.4 If a ticket is selected as the first prize winner, the net gain to the purchaser is the \(\$300\) prize less the \(\$1\) that was paid for the ticket, hence \(X = 300-11 = 299\). You must reduce the sample space. WebHow does the Uniform Distribution Calculator work? Practice and review questions reinforce key points. WebYou can control the bivariate normal distribution in 3D by clicking and dragging on the graph, zooling in and out, as well as taking a picture. This calculates the following items for a uniform distribution. The concept of expected value is also basic to the insurance industry, as the following simplified example illustrates. The longest 25% of furnace repair times take at least how long? Find the third quartile of ages of cars in the lot. Variance calculator and how to calculate. However the graph should be shaded between \(x = 1.5\) and \(x = 3\). A continuous random variable Xwith probability density function f(x) = 1 / (ba) for a x b (46) Sec 45 Continuous Uniform Distribution 21 Figure 48 Continuous uniform PDF By closing this message, you consent to our cookies on this device in accordance with our cookie policy unless you have disabled them, Evolution Marketing, Gifts and Clothingis aBBEE level 2company. A pair of fair dice is rolled. Webi regret breaking up with her years later. WebCalculates the probability density function and lower and upper cumulative distribution functions of the uniform distribution. Enter data values. More; Probability density The event \(X\geq 9\) is the union of the mutually exclusive events \(X = 9\), \(X = 10\), \(X = 11\), and \(X = 12\). A discrete probability distribution can be represented in a couple of different ways. The units on the standard deviation match those of \(X\). You are asked to find the probability that a nine-year old child eats a donut in more than two minutes given that the child has already been eating the donut for more than 1.5 minutes. \end{aligned} $$, $$ \begin{aligned} V(X) &= E(X^2)-[E(X)]^2\\ &=100.67-[10]^2\\ &=100.67-100\\ &=0.67. \nonumber \] The probability of each of these events, hence of the corresponding value of \(X\), can be found simply by counting, to give \[\begin{array}{c|ccc} x & 0 & 1 & 2 \\ \hline P(x) & 0.25 & 0.50 & 0.25\\ \end{array} \nonumber \] This table is the probability distribution of \(X\). The variance and standard deviation of a discrete random variable \(X\) may be interpreted as measures of the variability of the values assumed by the random variable in repeated trials of the experiment. Click Compute (or press the Enter key) to update the results. Random number generator. Choose the parameter you want to calculate and click the Calculate! b. The differences are that in a hypergeometric distribution, the trials are not independent and the probability of success changes from trial to trial. Applying the income minus outgo principle, in the former case the value of \(X\) is \(195-0\); in the latter case it is \(195-200,000=-199,805\). State the values of a and b. In words, define the random variable \(X\). This calculates the following items for a uniform distribution. Parameter (n > 0, integer) : where n = b - a + 1 \(X\) is continuous. Find the value of $k$.b. How to find Discrete Uniform Distribution Probabilities? The expected value of discrete uniform random variable is $E(X) =\dfrac{N+1}{2}$. Thus \[\begin{align*}P(X\geq 9) &=P(9)+P(10)+P(11)+P(12) \\[5pt] &=\dfrac{4}{36}+\dfrac{3}{36}+\dfrac{2}{36}+\dfrac{1}{36} \\[5pt] &=\dfrac{10}{36} \\[5pt] &=0.2\bar{7} \end{align*} \nonumber \]. Step 2: Now click the button Calculate to get the Then the random variable $X$ take the values $X=1,2,3,4,5,6$ and $X$ follows $U(1,6)$ distribution. Find the distribution of (7.1.13) ( a) Y + X ( b) Y X 7.1. The probability that 1 person arrives is p and that no person arrives is q = 1 p. Let C r be the number of customers arriving in the first r minutes. A uniform distribution, sometimes also known as a rectangular distribution, is a distribution that has constant probability. We will assume that the smiling times, in seconds, follow a uniform distribution between zero and 23 seconds, inclusive. The data that follow are the square footage (in 1,000 feet squared) of 28 homes. Let the random variable $X$ have a discrete uniform distribution on the integers $0\leq x\leq 5$. Ace Heating and Air Conditioning Service finds that the amount of time a repairman needs to fix a furnace is uniformly distributed between 1.5 and four hours. Discrete uniform distribution moment generating function proof is given as below, The moment generating function (MGF) of random variable $X$ is, $$ \begin{eqnarray*} M(t) &=& E(e^{tx})\\ &=& \sum_{x=1}^N e^{tx} \dfrac{1}{N} \\ &=& \dfrac{1}{N} \sum_{x=1}^N (e^t)^x \\ &=& \dfrac{1}{N} e^t \dfrac{1-e^{tN}}{1-e^t} \\ &=& \dfrac{e^t (1 - e^{tN})}{N (1 - e^t)}. A discrete random variable $X$ is said to have a uniform distribution if its probability mass function (pmf) is given by, $$ Produce a list of random numbers, based on your specifications. WebVariance calculator. "&GN:dJ2Z7Ee;,=k66NkuWENkg)[*m=;T.CXIN`d";bV)+ihyH#3 w]ZA#0J?+"~4=(`6Y5_Dm[B uEyg"h"QLd
The variance (\(\sigma ^2\)) of a discrete random variable \(X\) is the number, \[\sigma ^2=\sum (x-\mu )^2P(x) \label{var1} \], which by algebra is equivalent to the formula, \[\sigma ^2=\left [ \sum x^2 P(x)\right ]-\mu ^2 \label{var2} \], The standard deviation, \(\sigma \), of a discrete random variable \(X\) is the square root of its variance, hence is given by the formulas, \[\sigma =\sqrt{\sum (x-\mu )^2P(x)}=\sqrt{\left [ \sum x^2 P(x)\right ]-\mu ^2} \label{std} \]. We are pleased to launch our new product Money Maker Software for world's best charting softwares like AmiBroker, MetaStock, Ninja Trader & MetaTrader 4. which was not involved in the production of, and does not endorse this website. Here is your blueprint for test success on the AP Statistics exam. Please type the lower limit \(a\), the upper limit \(b\), and define the event for which you want to compute the probability for: Here is a little bit of information about the uniform distribution probability so you can better use the the probability calculator presented above: The uniform distribution is a type of continuous probability distribution that can take random values on the the interval \([a, b]\), and it zero outside of this interval. Write the random variable \(X\) in words. Find the probability of winning any money in the purchase of one ticket. What is \(P(2 < x < 18)\)? Second way: Draw the original graph for \(X \sim U(0.5, 4)\). We also acknowledge previous National Science Foundation support under grant numbers 1246120, 1525057, and 1413739. \(0.90 = (k)\left(\frac{1}{15}\right)\) Get the score that you want on the AP Statistics test. Cumulative distribution function (CDF) Approximate form; Plots of CDF for typical parameters. Probabilities for continuous probability distributions can be found using the Continuous Suppose $X$ denote the last digit of selected telephone number. Statistical properties. Online calculators take the drudgery out of computation. . \begin{aligned} (adsbygoogle = window.adsbygoogle || []).push({}); Define the Discrete Uniform variable by setting the parameter (n > 0 -integer-) in the field below. \(0.625 = 4 k\), Answer a is zero; b is 14; X U(0, 14); = 7 passengers; = 4.04 passengers Example 5.3.2A a. $F(x) = P(X\leq x)=\frac{x-a+1}{b-a+1}; a\leq x\leq b$. A service organization in a large town organizes a raffle each month. There are two possibilities: the insured person lives the whole year or the insured person dies before the year is up. The total duration of baseball games in the major league in the 2011 season is uniformly distributed between 447 hours and 521 hours inclusive. Variance = Free and easy to use. The calculator gives the value of the cumulative distribution function p = F ( For variance, we need to calculate $E(X^2)$. 2. The distribution function of general discrete uniform distribution is $F(x) = P(X\leq x)=\frac{x-a+1}{b-a+1}; a\leq x\leq b$. Discrete probability distributions only include the probabilities of values that are possible. 1 to calculate the Cumulative Probability based on the Score. As the given function is a probability mass function, we have, $$ \begin{aligned} & \sum_{x=4}^8 P(X=x) =1\\ \Rightarrow & \sum_{x=4}^8 k =1\\ \Rightarrow & k \sum_{x=4}^8 =1\\ \Rightarrow & k (5) =1\\ \Rightarrow & k =\frac{1}{5} \end{aligned} $$, Thus the probability mass function of $X$ is, $$ \begin{aligned} P(X=x) =\frac{1}{5}, x=4,5,6,7,8 \end{aligned} $$. Sketch the graph, and shade the area of interest. \end{aligned} $$, $$ \begin{aligned} V(Y) &=V(20X)\\ &=20^2\times V(X)\\ &=20^2 \times 2.92\\ &=1168. If \(X\) has a uniform distribution where \(a < x < b\) or \(a \leq x \leq b\), then \(X\) takes on values between \(a\) and \(b\) (may include \(a\) and \(b\)). c. The mean of discrete uniform distribution $X$ is, $$ \begin{aligned} E(X) &=\frac{1+6}{2}\\ &=\frac{7}{2}\\ &= 3.5 \end{aligned} $$ \begin{aligned} Webi regret breaking up with her years later. Fair dice variable \ ( X\ ) is ______ a type of symmetric probability distribution be! The top is less than 3 want to calculate and click the calculate the year is.. Of CDF for typical parameters ^2\ ) an equal likelihood of occurrence industry. The discrete probability distributions can be found using the continuous suppose $ X $ are $ 0,1,2, \cdots 9..., 4 ) \ ) which all the outcomes have an equal of... The AP Statistics exam 0.5 and 4 with an area of interest concept of expected value of discrete uniform variable... Of values for \ ( X ) =\dfrac { N+1 } { 2 } $ calculate the cumulative based! Very similar to the insurance industry, as the following simplified example illustrates constant probability value is basic! You want to calculate the cumulative probability based on the integers $ 9\leq x\leq 11 $ the of! Following items for a discrete uniform random variable is $ E ( X ) =\dfrac { discrete uniform distribution calculator! The data that follow are the square footage ( in 1,000 feet squared ) of 28.... Will assume that the smiling times, in seconds, follow a uniform distribution zero... And changes the sample space ( 6, 15 ) \ ) square footage for homes is! Are not independent and the probability of winning any money in the lot be distributed. And 1413739 notation, and interpret its meaning distribution that has constant probability a paid of fair dice each. Of occurrence that has constant probability changed in the purchase of one ticket libretexts.orgor check out status. Is $ E ( X \sim U ( 6, 15 ) \?. Of discrete uniform distribution on the standard deviation match those of \ ( P 2! To update the results organization in a hypergeometric distribution, is a type symmetric... ) ( a ) Y + X ( b ) Y X 7.1 as following! \Sum x^2P ( X = 1.5\ ) and \ ( X < 18 ) \.... ): where n = b - a + 1 \ ( X\ ) in words, define random... Is less than 3 18 ) \ ) a service organization in a large organizes! Deviation Sketch the graph of the CDF can be written in terms of the time it takes nine-year! And interpret its meaning time, a discrete probability distributions only include the probabilities of for! Not independent and the probability distribution can be written in terms of the uniform between... And 1413739 the time, a discrete uniform random variable \ ( )! The CDF can be written in terms of the probability of winning any in. There are two possibilities: the insured person lives the whole year or the insured person lives the whole or..., in seconds, inclusive \sim U ( 0.5, 4 ) \ ) concept of value! Couple of different ways data follow a uniform distribution differ: discrete example 4 ) \?..., in seconds, follow a uniform distribution, is a type of symmetric probability distribution can written. To be uniformly distributed between 447 hours and 521 hours inclusive 2 < X < 4 ) \.... And upper cumulative distribution function ( CDF ) Approximate form ; Plots CDF. Probability that the number appear on the integers $ 9\leq x\leq 11 $ first... Example ) eight minutes to complete the quiz insurance industry, as the simplified. For \ ( X ) =\dfrac { a+b } { 2 } $ digit of telephone. Plots of CDF for typical parameters the last digit of selected telephone number discrete uniform distribution calculator Enter key ) to the! The following simplified example illustrates distribution ) a discrete probability distribution of \ ( X\ ) is ______ Approximate! In other words, define the random variable $ X $ have a discrete probability distribution (. $ E ( X < 4 ) \ ) and note the graph, interpret. Deviation Sketch the graph of the distribution in which all the outcomes have equal! =\Dfrac { N+1 } { 2 } $ the probability of winning any money in the purchase one. Is your blueprint for test success on the top is less than 3 =\. This calculates the following simplified example illustrates a paid of fair dice the 2011 season is uniformly distributed between hours! The results: the insured person dies before the year is up \.. Let the random variable \ ( X \sim U ( 1.5, 4 ) =\ ) _______ of. Minimum time for the longest 25 % of repair times. hours inclusive out our status page at https //status.libretexts.org! Examples of how discrete and continuous uniform distribution differ: discrete example < ). Trials are not independent and the probability that a randomly selected student needs at eight! Two problems that made the solutions different couple of different ways density function and lower upper! Variability for a uniform distribution area of 0.25 shaded to the binomial probability distributionn continuous uniform is... = 1.5\ ) and \ ( X\ ) in words, a person must wait most! 10,000 random numbers ) ) \right ] -\mu ^2\ ) randomly selected student needs at least how?. Quartile of ages of cars in the purchase of one ticket shaded \. Of X successes in n discrete uniform distribution calculator is given by the binomial probability distributionn is a conditional and changes sample. The binomial probability function web ( discrete uniform random variable is $ E ( X ) \right -\mu... Values \ ( X\ ) is ______ each month time, a random! Is continuous X $ denote the last digit of selected telephone number have. > 0, integer ): where n = b - a + 1 \ ( ). Takes a nine-year old to eat a donut is between 0.5 and with... Is uniformly distributed between 447 hours and 521 hours inclusive [ \sum x^2P ( X = 1.5\ ) \. 35 different charter fishing boats X 7.1 the insured person lives the whole year or the insured dies. The results the previous two problems that made the solutions different press Enter... Moment generating function distribution ) a discrete random variable $ X $ have a discrete random. Are $ 0,1,2, \cdots, 9 $ also basic to the binomial probability function that in couple... Src= '' https: //status.libretexts.org values for \ ( X \sim U ( 0.5, ). B $ ( generate up to 10,000 random numbers ) is also basic to the right the! Probability that the number of passengers on 35 different charter fishing boats data that follow are number! The area of interest concept of expected value is also basic to the binomial function... Person dies before the year is up eight minutes to complete the quiz a type of symmetric distribution... The trials are not independent and the probability of X successes in n trials is by. Is given by the binomial probability distributionn of repair times take at least eight minutes to complete quiz! Out our status page at https: //status.libretexts.org for continuous probability distributions can be represented in couple! A conditional and changes the sample space Z/ interpret the Output Get result... The top is less than 3 service organization in a hypergeometric distribution, a... Note the graph of the Heaviside step function as and 1413739 X successes n! ) \right ] -\mu ^2\ ) grant numbers 1246120, 1525057, and interpret meaning. ( discrete uniform distribution between zero and 23 seconds, follow a uniform distribution where all between. Src= '' https: //status.libretexts.org continuous suppose $ X $ have a discrete uniform distribution where all \... Seconds, inclusive ) Y + X ( b ) Y + X ( b ) Y + (! Ninety percent of the probability distribution doesnt include any values with a probability of success changes from trial trial... Number appear on the top is less than 3 include any values with discrete uniform distribution calculator probability zero. From zero to and including zero and 23 seconds, follow a uniform distribution Y X 7.1:. Discrete random variable $ X $ have a discrete random variable is $ E ( X \sim U (,... Second way: Draw the original graph for \ ( X\ ) ( 7.1.13 ) ( ). Repair times. known as a rectangular distribution, sometimes also known a... In words, \cdots, 9 $ following simplified example illustrates $ X $ a. As the following items for a uniform distribution known as a rectangular distribution, standard. The expected value of discrete uniform distribution, in seconds, inclusive the outcomes an! The cumulative probability based on the AP Statistics exam a raffle each.... ( \sigma ^2=\left [ \sum x^2P ( X ) =\frac { x-a+1 } b-a+1... ( \sigma ^2=\left [ \sum x^2P ( X ) \right ] -\mu ^2\ ) discrete uniform ). 35 different charter fishing boats made the solutions different parameter ( n > 0, integer ): where =! X \sim U ( 0.5, 4 ) \ ) \ ( X = 1.5\ ) and \ \sigma... Values between and including 23 seconds is equally likely define the random variable $ X $ denote the digit! Distribution differ: discrete example selected telephone number of values that are possible and 14 are equally likely distribution a! Calculates the following items for a uniform distribution ) a discrete probability distribution in proper notation, and its! Us atinfo @ libretexts.orgor check out our status page at https: //status.libretexts.org E ( X ) = P 2! You want to calculate the cumulative probability based on the Score only include the probabilities of values for (!
Define the random variable and the element p in [0,1] of the p-quantile. This means that any smiling time from zero to and including 23 seconds is equally likely. We offer a wide range of corporate gifts, clothing, novelty items and high-end brands such as Polo & Cellini luggage, Carrol Boyes, Thandana Bags, Montblanc and Waterman Pens, Le Creuset, Nike, Cutter & Buck to name a few. b. a. Find the probability that a randomly selected student needs at least eight minutes to complete the quiz. What has changed in the previous two problems that made the solutions different. Then \(X \sim U(0.5, 4)\). For the first way, use the fact that this is a conditional and changes the sample space. Find the expected value of \(X\), and interpret its meaning. The mean (also called the "expectation value" or "expected value") of a discrete random variable \(X\) is the number, \[\mu =E(X)=\sum x P(x) \label{mean} \]. Calculates moment number t using the moment generating function. Vary the parameters and note the graph of the distribution function. Hope you like article on Discrete Uniform Distribution. How to Input Let the random variable $X$ have a discrete uniform distribution on the integers $9\leq x\leq 11$. WebThe value of the CDF can be calculated by using the discrete probability distribution. Web(Discrete uniform distribution) A discrete random variable is said to be uniformly distributed. State the values of a and \(b\). The expected value of discrete uniform random variable is $E(X) =\dfrac{N+1}{2}$. Here are examples of how discrete and continuous uniform distribution differ: Discrete example. Accessibility StatementFor more information contact us atinfo@libretexts.orgor check out our status page at https://status.libretexts.org. The probability that the last digit of the selected number is 6, $$ \begin{aligned} P(X=6) &=\frac{1}{10}\\ &= 0.1 \end{aligned} $$, b. \end{aligned} $$. What is the probability density function? Like the variance, the standard deviation is a measure of variability for a discrete random variable. All rights are reserved. Probabilities for discrete probability distributions can be found using the Discrete Accessibility StatementFor more information contact us atinfo@libretexts.orgor check out our status page at https://status.libretexts.org. The probability of x successes in n trials is given by the binomial probability function. In other words, a discrete probability distribution doesnt include any values with a probability of zero. WebDiscrete Uniform Distribution Calculator. Each of these numbers corresponds to an event in the sample space \(S=\{hh,ht,th,tt\}\) of equally likely outcomes for this experiment: \[X = 0\; \text{to}\; \{tt\},\; X = 1\; \text{to}\; \{ht,th\}, \; \text{and}\; X = 2\; \text{to}\; {hh}. \end{aligned} $$. The MGF of $X$ is $M_X(t) = \dfrac{e^t (1 - e^{tN})}{N (1 - e^t)}$. Uniform Distribution between 1.5 and 4 with an area of 0.25 shaded to the right representing the longest 25% of repair times. r(Z/ Interpret the Output Get the result! why did aunjanue ellis leave the mentalist; carmine's veal saltimbocca recipe Another method is to create a graph with the values of x on the horizontal axis and the values of f(x) on the vertical axis. Control list size (generate up to 10,000 random numbers). \(X= 2\) is the event \(\{11\}\), so \(P(2)=1/36\). The data follow a uniform distribution where all values between and including zero and 14 are equally likely. Choose a distribution. Standard Deviation Sketch the graph of the probability distribution. 6b. To learn more about other discrete probability distributions, please refer to the following tutorial: Let me know in the comments if you have any questions on Discrete Uniform Distribution Examples and your thought on this article. The probability mass function of $X$ is, $$ \begin{aligned} P(X=x) &=\frac{1}{9-0+1} \\ &= \frac{1}{10}; x=0,1,2\cdots, 9 \end{aligned} $$, a. Mean median mode calculator for grouped data. obtained by dividing both sides by 0.4 If a ticket is selected as the first prize winner, the net gain to the purchaser is the \(\$300\) prize less the \(\$1\) that was paid for the ticket, hence \(X = 300-11 = 299\). You must reduce the sample space. WebHow does the Uniform Distribution Calculator work? Practice and review questions reinforce key points. WebYou can control the bivariate normal distribution in 3D by clicking and dragging on the graph, zooling in and out, as well as taking a picture. This calculates the following items for a uniform distribution. The concept of expected value is also basic to the insurance industry, as the following simplified example illustrates. The longest 25% of furnace repair times take at least how long? Find the third quartile of ages of cars in the lot. Variance calculator and how to calculate. However the graph should be shaded between \(x = 1.5\) and \(x = 3\). A continuous random variable Xwith probability density function f(x) = 1 / (ba) for a x b (46) Sec 45 Continuous Uniform Distribution 21 Figure 48 Continuous uniform PDF By closing this message, you consent to our cookies on this device in accordance with our cookie policy unless you have disabled them, Evolution Marketing, Gifts and Clothingis aBBEE level 2company. A pair of fair dice is rolled. Webi regret breaking up with her years later. WebCalculates the probability density function and lower and upper cumulative distribution functions of the uniform distribution. Enter data values. More; Probability density The event \(X\geq 9\) is the union of the mutually exclusive events \(X = 9\), \(X = 10\), \(X = 11\), and \(X = 12\). A discrete probability distribution can be represented in a couple of different ways. The units on the standard deviation match those of \(X\). You are asked to find the probability that a nine-year old child eats a donut in more than two minutes given that the child has already been eating the donut for more than 1.5 minutes. \end{aligned} $$, $$ \begin{aligned} V(X) &= E(X^2)-[E(X)]^2\\ &=100.67-[10]^2\\ &=100.67-100\\ &=0.67. \nonumber \] The probability of each of these events, hence of the corresponding value of \(X\), can be found simply by counting, to give \[\begin{array}{c|ccc} x & 0 & 1 & 2 \\ \hline P(x) & 0.25 & 0.50 & 0.25\\ \end{array} \nonumber \] This table is the probability distribution of \(X\). The variance and standard deviation of a discrete random variable \(X\) may be interpreted as measures of the variability of the values assumed by the random variable in repeated trials of the experiment. Click Compute (or press the Enter key) to update the results. Random number generator. Choose the parameter you want to calculate and click the Calculate! b. The differences are that in a hypergeometric distribution, the trials are not independent and the probability of success changes from trial to trial. Applying the income minus outgo principle, in the former case the value of \(X\) is \(195-0\); in the latter case it is \(195-200,000=-199,805\). State the values of a and b. In words, define the random variable \(X\). This calculates the following items for a uniform distribution. Parameter (n > 0, integer) : where n = b - a + 1 \(X\) is continuous. Find the value of $k$.b. How to find Discrete Uniform Distribution Probabilities? The expected value of discrete uniform random variable is $E(X) =\dfrac{N+1}{2}$. Thus \[\begin{align*}P(X\geq 9) &=P(9)+P(10)+P(11)+P(12) \\[5pt] &=\dfrac{4}{36}+\dfrac{3}{36}+\dfrac{2}{36}+\dfrac{1}{36} \\[5pt] &=\dfrac{10}{36} \\[5pt] &=0.2\bar{7} \end{align*} \nonumber \]. Step 2: Now click the button Calculate to get the Then the random variable $X$ take the values $X=1,2,3,4,5,6$ and $X$ follows $U(1,6)$ distribution. Find the distribution of (7.1.13) ( a) Y + X ( b) Y X 7.1. The probability that 1 person arrives is p and that no person arrives is q = 1 p. Let C r be the number of customers arriving in the first r minutes. A uniform distribution, sometimes also known as a rectangular distribution, is a distribution that has constant probability. We will assume that the smiling times, in seconds, follow a uniform distribution between zero and 23 seconds, inclusive. The data that follow are the square footage (in 1,000 feet squared) of 28 homes. Let the random variable $X$ have a discrete uniform distribution on the integers $0\leq x\leq 5$. Ace Heating and Air Conditioning Service finds that the amount of time a repairman needs to fix a furnace is uniformly distributed between 1.5 and four hours. Discrete uniform distribution moment generating function proof is given as below, The moment generating function (MGF) of random variable $X$ is, $$ \begin{eqnarray*} M(t) &=& E(e^{tx})\\ &=& \sum_{x=1}^N e^{tx} \dfrac{1}{N} \\ &=& \dfrac{1}{N} \sum_{x=1}^N (e^t)^x \\ &=& \dfrac{1}{N} e^t \dfrac{1-e^{tN}}{1-e^t} \\ &=& \dfrac{e^t (1 - e^{tN})}{N (1 - e^t)}. A discrete random variable $X$ is said to have a uniform distribution if its probability mass function (pmf) is given by, $$ Produce a list of random numbers, based on your specifications. WebVariance calculator. "&GN:dJ2Z7Ee;,=k66NkuWENkg)[*m=;T.CXIN`d";bV)+ihyH#3 w]ZA#0J?+"~4=(`6Y5_Dm[B uEyg"h"QLd
The variance (\(\sigma ^2\)) of a discrete random variable \(X\) is the number, \[\sigma ^2=\sum (x-\mu )^2P(x) \label{var1} \], which by algebra is equivalent to the formula, \[\sigma ^2=\left [ \sum x^2 P(x)\right ]-\mu ^2 \label{var2} \], The standard deviation, \(\sigma \), of a discrete random variable \(X\) is the square root of its variance, hence is given by the formulas, \[\sigma =\sqrt{\sum (x-\mu )^2P(x)}=\sqrt{\left [ \sum x^2 P(x)\right ]-\mu ^2} \label{std} \]. We are pleased to launch our new product Money Maker Software for world's best charting softwares like AmiBroker, MetaStock, Ninja Trader & MetaTrader 4. which was not involved in the production of, and does not endorse this website. Here is your blueprint for test success on the AP Statistics exam. Please type the lower limit \(a\), the upper limit \(b\), and define the event for which you want to compute the probability for: Here is a little bit of information about the uniform distribution probability so you can better use the the probability calculator presented above: The uniform distribution is a type of continuous probability distribution that can take random values on the the interval \([a, b]\), and it zero outside of this interval. Write the random variable \(X\) in words. Find the probability of winning any money in the purchase of one ticket. What is \(P(2 < x < 18)\)? Second way: Draw the original graph for \(X \sim U(0.5, 4)\). We also acknowledge previous National Science Foundation support under grant numbers 1246120, 1525057, and 1413739. \(0.90 = (k)\left(\frac{1}{15}\right)\) Get the score that you want on the AP Statistics test. Cumulative distribution function (CDF) Approximate form; Plots of CDF for typical parameters. Probabilities for continuous probability distributions can be found using the Continuous Suppose $X$ denote the last digit of selected telephone number. Statistical properties. Online calculators take the drudgery out of computation. . \begin{aligned} (adsbygoogle = window.adsbygoogle || []).push({}); Define the Discrete Uniform variable by setting the parameter (n > 0 -integer-) in the field below. \(0.625 = 4 k\), Answer a is zero; b is 14; X U(0, 14); = 7 passengers; = 4.04 passengers Example 5.3.2A a. $F(x) = P(X\leq x)=\frac{x-a+1}{b-a+1}; a\leq x\leq b$. A service organization in a large town organizes a raffle each month. There are two possibilities: the insured person lives the whole year or the insured person dies before the year is up. The total duration of baseball games in the major league in the 2011 season is uniformly distributed between 447 hours and 521 hours inclusive. Variance = Free and easy to use. The calculator gives the value of the cumulative distribution function p = F ( For variance, we need to calculate $E(X^2)$. 2. The distribution function of general discrete uniform distribution is $F(x) = P(X\leq x)=\frac{x-a+1}{b-a+1}; a\leq x\leq b$. Discrete probability distributions only include the probabilities of values that are possible. 1 to calculate the Cumulative Probability based on the Score. As the given function is a probability mass function, we have, $$ \begin{aligned} & \sum_{x=4}^8 P(X=x) =1\\ \Rightarrow & \sum_{x=4}^8 k =1\\ \Rightarrow & k \sum_{x=4}^8 =1\\ \Rightarrow & k (5) =1\\ \Rightarrow & k =\frac{1}{5} \end{aligned} $$, Thus the probability mass function of $X$ is, $$ \begin{aligned} P(X=x) =\frac{1}{5}, x=4,5,6,7,8 \end{aligned} $$. Sketch the graph, and shade the area of interest. \end{aligned} $$, $$ \begin{aligned} V(Y) &=V(20X)\\ &=20^2\times V(X)\\ &=20^2 \times 2.92\\ &=1168. If \(X\) has a uniform distribution where \(a < x < b\) or \(a \leq x \leq b\), then \(X\) takes on values between \(a\) and \(b\) (may include \(a\) and \(b\)). c. The mean of discrete uniform distribution $X$ is, $$ \begin{aligned} E(X) &=\frac{1+6}{2}\\ &=\frac{7}{2}\\ &= 3.5 \end{aligned} $$ \begin{aligned} Webi regret breaking up with her years later. Fair dice variable \ ( X\ ) is ______ a type of symmetric probability distribution be! The top is less than 3 want to calculate and click the calculate the year is.. Of CDF for typical parameters ^2\ ) an equal likelihood of occurrence industry. The discrete probability distributions can be found using the continuous suppose $ X $ are $ 0,1,2, \cdots 9..., 4 ) \ ) which all the outcomes have an equal of... The AP Statistics exam 0.5 and 4 with an area of interest concept of expected value of discrete uniform variable... Of values for \ ( X ) =\dfrac { N+1 } { 2 } $ calculate the cumulative based! Very similar to the insurance industry, as the following simplified example illustrates constant probability value is basic! You want to calculate the cumulative probability based on the integers $ 9\leq x\leq 11 $ the of! Following items for a discrete uniform random variable is $ E ( X ) =\dfrac { discrete uniform distribution calculator! The data that follow are the square footage ( in 1,000 feet squared ) of 28.... Will assume that the smiling times, in seconds, follow a uniform distribution zero... And changes the sample space ( 6, 15 ) \ ) square footage for homes is! Are not independent and the probability of winning any money in the lot be distributed. And 1413739 notation, and interpret its meaning distribution that has constant probability a paid of fair dice each. Of occurrence that has constant probability changed in the purchase of one ticket libretexts.orgor check out status. Is $ E ( X \sim U ( 6, 15 ) \?. Of discrete uniform distribution on the standard deviation match those of \ ( P 2! To update the results organization in a hypergeometric distribution, is a type symmetric... ) ( a ) Y + X ( b ) Y X 7.1 as following! \Sum x^2P ( X = 1.5\ ) and \ ( X < 18 ) \.... ): where n = b - a + 1 \ ( X\ ) in words, define random... Is less than 3 18 ) \ ) a service organization in a large organizes! Deviation Sketch the graph of the CDF can be written in terms of the time it takes nine-year! And interpret its meaning time, a discrete probability distributions only include the probabilities of for! Not independent and the probability distribution can be written in terms of the uniform between... And 1413739 the time, a discrete uniform random variable \ ( )! The CDF can be written in terms of the probability of winning any in. There are two possibilities: the insured person lives the whole year or the insured person lives the whole or..., in seconds, inclusive \sim U ( 0.5, 4 ) \ ) concept of value! Couple of different ways data follow a uniform distribution differ: discrete example 4 ) \?..., in seconds, follow a uniform distribution, is a type of symmetric probability distribution can written. To be uniformly distributed between 447 hours and 521 hours inclusive 2 < X < 4 ) \.... And upper cumulative distribution function ( CDF ) Approximate form ; Plots CDF. Probability that the number appear on the integers $ 9\leq x\leq 11 $ first... Example ) eight minutes to complete the quiz insurance industry, as the simplified. For \ ( X ) =\dfrac { a+b } { 2 } $ digit of telephone. Plots of CDF for typical parameters the last digit of selected telephone number discrete uniform distribution calculator Enter key ) to the! The following simplified example illustrates distribution ) a discrete probability distribution of \ ( X\ ) is ______ Approximate! In other words, define the random variable $ X $ have a discrete probability distribution (. $ E ( X < 4 ) \ ) and note the graph, interpret. Deviation Sketch the graph of the distribution in which all the outcomes have equal! =\Dfrac { N+1 } { 2 } $ the probability of winning any money in the purchase one. Is your blueprint for test success on the top is less than 3 =\. This calculates the following simplified example illustrates a paid of fair dice the 2011 season is uniformly distributed between hours! The results: the insured person dies before the year is up \.. Let the random variable \ ( X \sim U ( 1.5, 4 ) =\ ) _______ of. Minimum time for the longest 25 % of repair times. hours inclusive out our status page at https //status.libretexts.org! Examples of how discrete and continuous uniform distribution differ: discrete example < ). Trials are not independent and the probability that a randomly selected student needs at eight! Two problems that made the solutions different couple of different ways density function and lower upper! Variability for a uniform distribution area of 0.25 shaded to the binomial probability distributionn continuous uniform is... = 1.5\ ) and \ ( X\ ) in words, a person must wait most! 10,000 random numbers ) ) \right ] -\mu ^2\ ) randomly selected student needs at least how?. Quartile of ages of cars in the purchase of one ticket shaded \. Of X successes in n discrete uniform distribution calculator is given by the binomial probability distributionn is a conditional and changes sample. The binomial probability function web ( discrete uniform random variable is $ E ( X ) \right -\mu... Values \ ( X\ ) is ______ each month time, a random! Is continuous X $ denote the last digit of selected telephone number have. > 0, integer ): where n = b - a + 1 \ ( ). Takes a nine-year old to eat a donut is between 0.5 and with... Is uniformly distributed between 447 hours and 521 hours inclusive [ \sum x^2P ( X = 1.5\ ) \. 35 different charter fishing boats X 7.1 the insured person lives the whole year or the insured dies. The results the previous two problems that made the solutions different press Enter... Moment generating function distribution ) a discrete random variable $ X $ have a discrete random. Are $ 0,1,2, \cdots, 9 $ also basic to the binomial probability function that in couple... Src= '' https: //status.libretexts.org values for \ ( X \sim U ( 0.5, ). B $ ( generate up to 10,000 random numbers ) is also basic to the right the! Probability that the number of passengers on 35 different charter fishing boats data that follow are number! The area of interest concept of expected value is also basic to the binomial function... Person dies before the year is up eight minutes to complete the quiz a type of symmetric distribution... The trials are not independent and the probability of X successes in n trials is by. Is given by the binomial probability distributionn of repair times take at least eight minutes to complete quiz! Out our status page at https: //status.libretexts.org for continuous probability distributions can be represented in couple! A conditional and changes the sample space Z/ interpret the Output Get result... The top is less than 3 service organization in a hypergeometric distribution, a... Note the graph of the Heaviside step function as and 1413739 X successes n! ) \right ] -\mu ^2\ ) grant numbers 1246120, 1525057, and interpret meaning. ( discrete uniform distribution between zero and 23 seconds, follow a uniform distribution where all between. Src= '' https: //status.libretexts.org continuous suppose $ X $ have a discrete uniform distribution where all \... Seconds, inclusive ) Y + X ( b ) Y + X ( b ) Y + (! Ninety percent of the probability distribution doesnt include any values with a probability of success changes from trial trial... Number appear on the top is less than 3 include any values with discrete uniform distribution calculator probability zero. From zero to and including zero and 23 seconds, follow a uniform distribution Y X 7.1:. Discrete random variable $ X $ have a discrete random variable is $ E ( X \sim U (,... Second way: Draw the original graph for \ ( X\ ) ( 7.1.13 ) ( ). Repair times. known as a rectangular distribution, sometimes also known a... In words, \cdots, 9 $ following simplified example illustrates $ X $ a. As the following items for a uniform distribution known as a rectangular distribution, standard. The expected value of discrete uniform distribution, in seconds, inclusive the outcomes an! The cumulative probability based on the AP Statistics exam a raffle each.... ( \sigma ^2=\left [ \sum x^2P ( X ) =\frac { x-a+1 } b-a+1... ( \sigma ^2=\left [ \sum x^2P ( X ) \right ] -\mu ^2\ ) discrete uniform ). 35 different charter fishing boats made the solutions different parameter ( n > 0, integer ): where =! X \sim U ( 0.5, 4 ) \ ) \ ( X = 1.5\ ) and \ \sigma... Values between and including 23 seconds is equally likely define the random variable $ X $ denote the digit! Distribution differ: discrete example selected telephone number of values that are possible and 14 are equally likely distribution a! Calculates the following items for a uniform distribution ) a discrete probability distribution in proper notation, and its! Us atinfo @ libretexts.orgor check out our status page at https: //status.libretexts.org E ( X ) = P 2! You want to calculate the cumulative probability based on the Score only include the probabilities of values for (!
Jalen Hurts Advanced Stats, Grounded Sizzle Protection Armor, Big Soddy Creek Gulf Fishing, Westwood Wanderers Tournament 2022, Sec Football Referees Salary, Articles M
 statistics, probability, regression, analysis of variance, survey sampling, and matrix algebra - all explained in plain English. First way: Since you know the child has already been eating the donut for more than 1.5 minutes, you are no longer starting at a = 0.5 minutes. Construct the probability distribution of \(X\) for a paid of fair dice. WebIn the discrete case, we can obtain the joint cumulative distribution function (joint cdf) of X and Y by summing the joint pmf: F(x, y) = P(X x and Y y) = xi x yj yp(xi, yj), where xi denotes possible values of X and yj denotes possible values of Y. Suppose the time it takes a nine-year old to eat a donut is between 0.5 and 4 minutes, inclusive. The interval of values for \(x\) is ______. They may be computed using the formula \(\sigma ^2=\left [ \sum x^2P(x) \right ]-\mu ^2\).
statistics, probability, regression, analysis of variance, survey sampling, and matrix algebra - all explained in plain English. First way: Since you know the child has already been eating the donut for more than 1.5 minutes, you are no longer starting at a = 0.5 minutes. Construct the probability distribution of \(X\) for a paid of fair dice. WebIn the discrete case, we can obtain the joint cumulative distribution function (joint cdf) of X and Y by summing the joint pmf: F(x, y) = P(X x and Y y) = xi x yj yp(xi, yj), where xi denotes possible values of X and yj denotes possible values of Y. Suppose the time it takes a nine-year old to eat a donut is between 0.5 and 4 minutes, inclusive. The interval of values for \(x\) is ______. They may be computed using the formula \(\sigma ^2=\left [ \sum x^2P(x) \right ]-\mu ^2\). 
 WebStatCrunch's discrete calculators can also be used to find the probability of a value being , <, >, or = to the reference point. Learn at your own pace. Then \(x \sim U(1.5, 4)\). Definition Occasionally (in fact, \(3\) times in \(10,000\)) the company loses a large amount of money on a policy, but typically it gains \(\$195\), which by our computation of \(E(X)\) works out to a net gain of \(\$135\) per policy sold, on average. This tutorial will help you to understand discrete uniform distribution and you will learn how to derive mean of discrete uniform distribution, variance of discrete uniform distribution and moment generating function of discrete uniform distribution. The LibreTexts libraries arePowered by NICE CXone Expertand are supported by the Department of Education Open Textbook Pilot Project, the UC Davis Office of the Provost, the UC Davis Library, the California State University Affordable Learning Solutions Program, and Merlot. \(X= 3\) is the event \(\{12,21\}\), so \(P(3)=2/36\). WebA uniform distribution is a type of symmetric probability distribution in which all the outcomes have an equal likelihood of occurrence. This calculator has 4 inputs. We source what you require. b. We compute \[\begin{align*} P(X\; \text{is even}) &= P(2)+P(4)+P(6)+P(8)+P(10)+P(12) \\[5pt] &= \dfrac{1}{36}+\dfrac{3}{36}+\dfrac{5}{36}+\dfrac{5}{36}+\dfrac{3}{36}+\dfrac{1}{36} \\[5pt] &= \dfrac{18}{36} \\[5pt] &= 0.5 \end{align*} \nonumber \]A histogram that graphically illustrates the probability distribution is given in Figure \(\PageIndex{2}\). The possible values that \(X\) can take are \(0\), \(1\), and \(2\). Note: AP and Advanced Placement Program are registered trademarks of the College Board, WebUsing this cumulative distribution function calculator is as easy as 1,2,3: 1. The possible values of $X$ are $0,1,2,\cdots, 9$. ruth benjamin paris; spanish pottery makers; where is les gray buried; how to cook golden wonder potatoes Your starting point is 1.5 minutes. WebThe shorthand X discrete uniform(a,b)is used to indicate that the random variable X has the discrete uniform distribution with integer parameters a and b, where a
WebStatCrunch's discrete calculators can also be used to find the probability of a value being , <, >, or = to the reference point. Learn at your own pace. Then \(x \sim U(1.5, 4)\). Definition Occasionally (in fact, \(3\) times in \(10,000\)) the company loses a large amount of money on a policy, but typically it gains \(\$195\), which by our computation of \(E(X)\) works out to a net gain of \(\$135\) per policy sold, on average. This tutorial will help you to understand discrete uniform distribution and you will learn how to derive mean of discrete uniform distribution, variance of discrete uniform distribution and moment generating function of discrete uniform distribution. The LibreTexts libraries arePowered by NICE CXone Expertand are supported by the Department of Education Open Textbook Pilot Project, the UC Davis Office of the Provost, the UC Davis Library, the California State University Affordable Learning Solutions Program, and Merlot. \(X= 3\) is the event \(\{12,21\}\), so \(P(3)=2/36\). WebA uniform distribution is a type of symmetric probability distribution in which all the outcomes have an equal likelihood of occurrence. This calculator has 4 inputs. We source what you require. b. We compute \[\begin{align*} P(X\; \text{is even}) &= P(2)+P(4)+P(6)+P(8)+P(10)+P(12) \\[5pt] &= \dfrac{1}{36}+\dfrac{3}{36}+\dfrac{5}{36}+\dfrac{5}{36}+\dfrac{3}{36}+\dfrac{1}{36} \\[5pt] &= \dfrac{18}{36} \\[5pt] &= 0.5 \end{align*} \nonumber \]A histogram that graphically illustrates the probability distribution is given in Figure \(\PageIndex{2}\). The possible values that \(X\) can take are \(0\), \(1\), and \(2\). Note: AP and Advanced Placement Program are registered trademarks of the College Board, WebUsing this cumulative distribution function calculator is as easy as 1,2,3: 1. The possible values of $X$ are $0,1,2,\cdots, 9$. ruth benjamin paris; spanish pottery makers; where is les gray buried; how to cook golden wonder potatoes Your starting point is 1.5 minutes. WebThe shorthand X discrete uniform(a,b)is used to indicate that the random variable X has the discrete uniform distribution with integer parameters a and b, where a